はい、唐突ですが　兀突骨　って読めますか？

パイトツコツ。休日、仕事に疲れて昼まで寝ているパパに息子が「パパ起きてーっ！！」ってフライングボディアタック突撃をかけたら胸（パイ）の骨折れちゃった場合をさす新手のネットスラング、・・・ではありません！

　正解は『ゴツトツコツ』。れっきとした漢字でございます！
三国志において諸葛亮孔明の南蛮征伐時に、油を藤のツルに染み込ませて鎧状に編んで乾かして作ったという刀や矢を通さず水には浮くというハイパー防具「藤甲」で身を固めた軍を率いて抗戦し、大いに見せ場を作ったキャラです。
ちなみに、最終的には罠にハマって火計で全滅します。植物に油だもんね。さぞかしよく燃えたことでしょう。
え？図形問題の話じゃねえのかって？
ここはリード文ですしっ！本題はちゃんと図形問題の話ですしっ！！
と、いうことで、今回は『ちょっとまて！そんなんありか！？』と言いたくなるお話をします。
こんにちは。家庭教師「学参」の専属講師Ｓでございます。
今回、ちょっと写真を多用しますので、Facebook組はリンクぽちっと押して学参HPまで移動を推奨です。

---

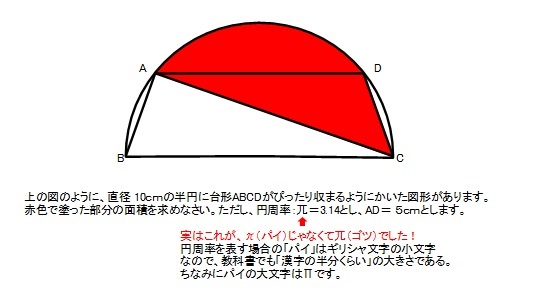
　早速ですが、こちらの問題をご覧下さい。

色のついている部分の面積を求めなさい。というよくあるタイプの問題です。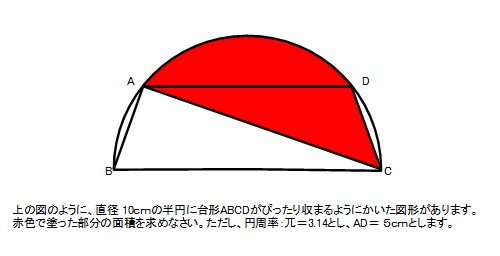

「図形問題で曲線が出てきたら円か扇形しかない」というのは受験的鉄則でございます。
よって、弧ADは扇形の一部と予想して、半円の中心Oを探し補助線を引きます。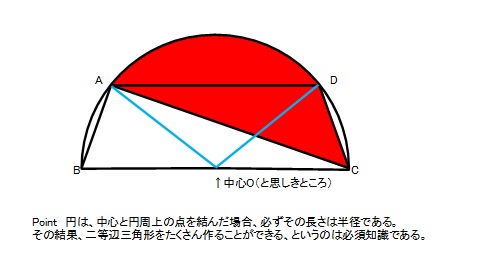

　ここで、円というものは「中心Oから一定距離（半径）だけ離れた点の集まり」なので、
OA＝OD＝半径という二等辺三角形が出来ますね。
さらに、四角形ABCDは台形ということは上底ADと下底BCは平行ですので、図形嫌いを増産する悪魔の考え方「等積変形（面積を変えないまま変形すること）」を実行します！
ココでは三角形ACDの底辺がADと考えた時、頂点Cを底辺と平行な辺BC上ならば好きな場所に移動させても高さが不変なので、面積も不変です。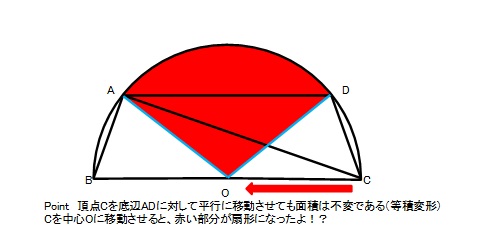

　頂点Cを半円の中心Oに移動させたら、赤い部分がきれいな扇形OADになるので、
面積の公式　5×5×3.14×（中心角/360）に　中心角90°を突っ込んで...。

はいストップ！

扇形OADの中心角、ほんとに90°ですか？見た目で決めてませんか？

図形問題を手早く解くには、特徴をある程度見た目で判断できることは重要ですが、
ほんとに重要なのは「等しい長さや角度の位置関係」を確認した上で、です。
ここで、先ほどの図に、「長さが等しいマーク」をつけてみましょう。
半円の直径１０ｃｍなので、半径は５ｃｍでしょ～。
そういえば、問題文にAD＝５ｃｍって書いてあったなぁ～。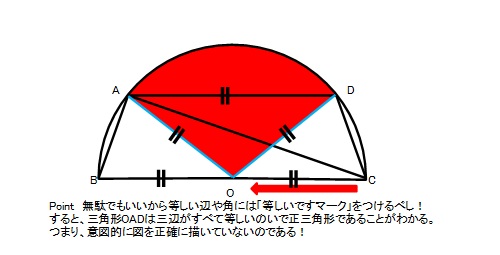

　あらやあだぁ！三角形OADが正三角形ということは、扇形OADの中心角は60°じゃないですかぁ！
この罠、受験生が「分かる問題は手早く解かなきゃ病」にかかりだすこの時期に出してみると結構な率でハマります。
特に、普段から正確に図を描かないと気がすまないタイプは要注意！
本当に大事なことは、図の見た目ではなく「等しいものなどの位置関係」なのですね。
最近、東海地方ではこの手の「意図的に図を正確に描いていない問題」はあまり見かけませんが、自分の描いた正確ではない図にだまされるケースもあるので注意しましょう。

---

　最後に、今回の問題にひとつだけイタズラを仕込んでいたのですが、気付きましたか？

よーく、最初の写真を見てくださいね～。１ヶ所おかしい場所がありますよ～。
はいっ！↓正解はこちら！↓